Project 1
Colorizing the Prokudin-Gorskii Photo Collection
Sergei Prokudin-Gorskii, a pioneer of color photography, captured thousands of images using a three-filter method. By combining separate red, green, and blue channels from glass plate negatives, we can recover full-color photographs. The goal of this project is to use image processing techniques to align these individual color channel images and generate full-color images with minimal visual artifacts.



Figure 1: Separate red, green, and blue channels from the glass plate negatives.
Formally, let $I_1(x, y)$ and $I_2(x, y)$ denote the pixel intensities of images $I_1$ and $I_2$ at $(x, y)$. We want to estimate a translation $(\Delta x, \Delta y)$ such that the transformed image $I_1$ is as close as possible to $I_2$. In other words, we solve the following optimization problem:
\[\Delta x^*, \Delta y^* = \underset{\Delta x, \Delta y}{\text{argmin}} \sum_{x, y} (I_1(x+\Delta x, y+\Delta y) - I_2(x, y))^2\]We can also use alternative distance metrics, such as mean absolute error or normalized cross-correlation, to measure the similarity between the transformed image and the reference image. For the remainder of our work, we will align the red and green channels to the blue channel.
Exhaustive search
The naive approach to solving the optimization problem is to optimize $(\Delta x, \Delta y)$ within a predefined search window. We implemented an exhaustive search algorithm that looks for the optimal translation in the space $[-15, 15]\times [-15, 15]$. This method works well for low-resolution images like cathedral, monastery, and tobolsk, which are around $256\times 256$ pixels in size.
Figure 2: Alignment result for low resolution images.
However, when applying this algorithm to align high-resolution images with dimensions around $3000 \times 3000$ pixels, performance deteriorates. One issue is that the search space $[-15, 15] \times [-15, 15]$ is too small. Increasing the search space, however, extends the runtime significantly, as the algorithm has quadratic time complexity.


Figure 3: Exhaustive search does not work well with high resolution images.
Multipyramid search
To improve the efficiency of the search, we can apply the algorithm to the pyramid representation of the images. In this representation, an image is represented at multiple resolutions through repetitive subsampling. By performing the search on low-resolution images first and refining the estimate as we progress to higher resolutions, we can enhance both accuracy and efficiency.
Figure 4: The image pyramid is constructed through repetitive subsampling. Blurring is often applied to avoid aliasing. [1]
In the implementation, we first create a Gaussian pyramid of the image by applying a Gaussian blur followed by subsampling with a factor of 2 at each level, until the image size is reduced to below $256 \times 256$. We then apply our search algorithm on the low-resolution image. Suppose the predicted translation is $(\Delta x, \Delta y)$. In the subsequent step, we perform the search on the next higher-resolution image using a search window defined as $[2\Delta x - \epsilon, 2\Delta x + \epsilon] \times [2\Delta y - \epsilon, 2\Delta y + \epsilon]$, where $\epsilon$ is set to 10 in our experiment.
Figure 4: Pyramid search performs well on most images.
SIFT-based image alignment
In our previous approach, we compared two images by measuring their distance, with various possible distance metrics. Another method for alignment involves extracting significant feature points and aligning these points instead. To extract these feature points, we use Scale-Invariant Feature Transform (SIFT). SIFT identifies distinctive feature points by locating maxima and minima in the scale-space pyramid. Subsequent preprocessing steps are applied to remove points with weak signals [2].


Figure 5: Keypoints and descriptors generated by SIFT. These can then be matched by finding nearest neighbors. (Left) Red channel (Right) Blue channels.
In this section, we used SIFT to extract feature points and their corresponding descriptors from both images. We then matched the feature points based on their descriptors using the k-nearest neighbors (kNN) algorithm with $k=2$. After matching the points, we fit a homography matrix to estimate the transformation.
Figure 6: SIFT based alignment works well for all images. Note that the results for emir and harvesting is much better.
Runtime comparison
The runtime analysis shows that the Pyramid search and SIFT methods exhibit similar performance levels. Both methods significantly outperform the Exhaustive search in terms of both execution time and alignment quality.
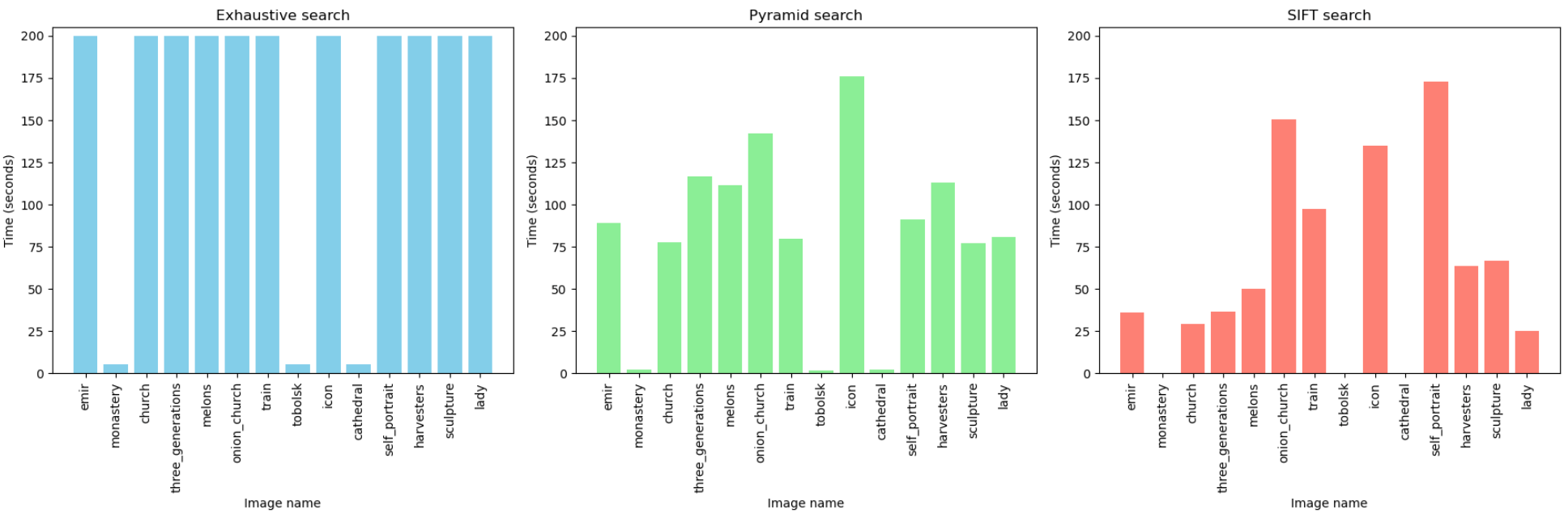
Figure 7: Time performance for three algorithms. For the exhasutive search, we stopped the algorithm after $200$ seconds. [1]
Bibliography
[1] Wikimedia Foundation. (2023, December 8). Pyramid (Image Processing). Wikipedia. https://en.wikipedia.org/wiki/Pyramid_(image_processing)#:~:text=In%20a%20Gaussian%20pyramid%2C%20subsequent,used%20especially%20in%20texture%20synthesis.
[2] Szeliski, R. (2022). Computer vision: Algorithms and applications. Springer International Publishing Springer.








































